Nombres complexes et logarithmes

PROJET G5

LES NOMBRES COMPLEXES SANS COMPLEXE

(complexe mais pas compliqué ! Cette notion est essentielle pour comprendre les calculs impliquant selfs et capacités)

Les nombres réels peuvent être représentés par une droite allant de – l’infini à + l’infini en passant par zéro.
Cette approche peut être considérée comme insuffisante pour représenter des valeurs plus complexes à deux dimensions . Les mathématiciens ont donc bâti un système correspondant en adoptant une deuxième droite dite droite des imaginaires dont la représentation est perpendiculaire à la droite des réels allant également de – l’infini à + l’infini en croisant l’axe des réels en zéro. Ainsi au lieu de disposer d’une droite infinie de valeurs nous disposons d’un plan infini de valeurs.

L’axe horizontal est l’axe des réels : l’unité OI = 1.
L’axe vertical est l’axe des imaginaires : l‘unité OJ = j.
La notation d’un nombre complexe quelconque est :

z = a + jb

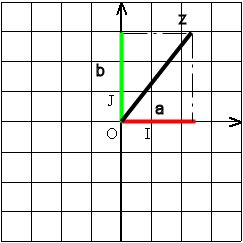
avec a = partie réelle du nombre complexe z
b = partie imaginaire du nombre complexe z

on appelle MODULE DE z : \(|z|=\sqrt{a^2+b^2}\)

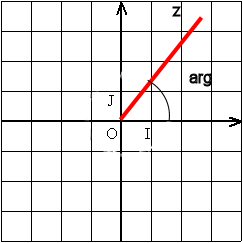
on appelle ARGUMENT DE z : \(arg(z)= arctg \frac{b}{a}\)

Le nombre complexe est donc caractérisé soit par ses coordonnées cartésiennes a et b soit par ses coordonnées polaires |z| et arg(z) . Ce dernier est l’angle que forme le vecteur z avec l’axe des réels

L’unité j peut s’écrire z = 0 + j = 1 x j c’est-à-dire le réel 1 multiplié par j . On voit sur l’image1 ci-dessous que multiplier par j revient à faire faire une rotation de PI/2ou 90° au nombre que l’on multiplie.

Si l’on multiplie encore z = j par j on obtient z = j² = – 1.

Cette rotation nous fait retrouver un réel pur : -1 ( image 2 ci-dessous) .

Une autre rotation donne z = -1 x j = -j ( = j puissance 3 ) qui est comme j un imaginaire pur


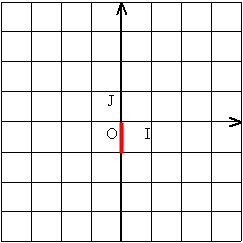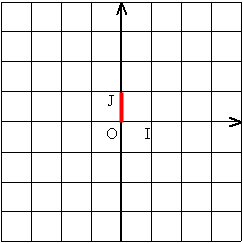
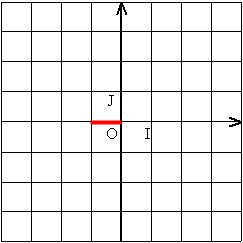
z = 1 x j	z = j² = – 1	z = -1 x j = – j

Il est inutile de retenir les formules qui suivent,seuls les principes sont à retenir

Somme de deux complexes :

z1 = a1 + jb1 + z2 = a2 + jb2 :

Z = z1 + z2 = a1 + a2 + j (b1 + b2)

( on additionne parties réelles et imaginaires )

Pour la différence on applique bien sûr le même principe. Pour les opérations de somme et différence on utilise obligatoirement les données cartésiennes.

Quotient de deux complexes :

z1 = a1 + jb1 et z2 = a2 + jb2

          a1 +  jb1
Z   =    ___________
          a2  +  jb2

On peut déterminer le quotient de deux complexes en passant par les coordonnées polaires des opérandes :

Principe à retenir :le module du quotient est le quotient des modules

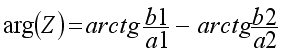
Principe à retenir : l’argument du quotient est la différence entre l’argument du numérateur et celui du dénominateur.

Produit de deux complexes :

En coordonnées cartésiennes : Z = z1.z2

= (a1 + jb1).(a2 + jb2) = a1a2 + ja2b1 + ja1b2 + j²b1b2 = a1a2-b1b2 + j (a1b2 + a2b1)

En coordonnées polaires

Principe à retenir : le module du produit est le produit des modules

Principe à retenir : l’argument du produit est la somme des arguments des deux termes

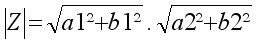
Conjugué d’un nombre complexe

Si z = a + jb le conjugué est a – jb . On voit que les parties imaginaires étant opposées , les arguments sont opposés.
Si l’on fait le produit des deux , les arguments s’annulant on obtiendra un nombre réel pur :

z. conjugé de z = (a+ jb).(a -jb) = a²+ b² + j (ab – ab)

(a + jb).(a- jb) = a² + b²

D’où l’on tire une autre manière de calculer le quotient de deux complexes en multipliant haut et bas par le conjugué du dénominateur :

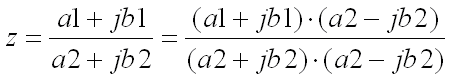
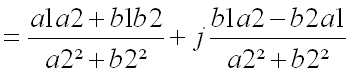
On peut développer indéfiniment sur les complexes mais pour les calculs en électronique les principes ci-dessus sont suffisants .

Il est bon de reconnaître cependant les pièges que l’on peut rencontrer dans ce type de calculs :

Ex : quelles sont les valeurs de b pour lesquelles nous avons | a + jb | = K et développer ainsi puisque K est un module c’est un réel pur alors K – a = jb .

Ceci est faux naturellement puisqu’il faut immédiatement écrire :

K = racine carrée de ( a²+b²)

LES LOGARITHMES A SON RYTHME

(le logarithme dont il est question ici est celui à base 10)

Nous savons que: 10 x 10 =10² = 100.

C’est exactement la même chose que d’écrire :log(100) = 2

De même log (1000) = 3 ; log (100000) = 5
etc ….

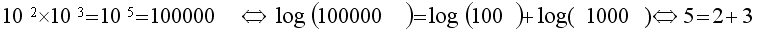
Alors quel intérêt ? C’est que lorsque l’on manipule des grandeurs disproportionnées il est plus simple d’ajouter que de multiplier. L’addition remplace la multiplication tout comme la soustraction remplace la division :

Si a x b = c alors log (a) + log (b) = log (c)

De même que 1000 / 10 = 100
log(1000) – log (10) = log (100)
( 3 – 1 = 2)
On peut alors écrire :

Si a / b = c alors log (a) – log (b) = log (c)

Cette notion de logarithme prend son sens lorsque l’on manipule les décibels (dB) qui expriment le gain d’un amplificateur ou l’atténuation d’un filtre et que l’on enchaîne plusieurs d’entre
eux.

Oui mais c’est facile quand on a affaire à une puissance de 10 mais quand c’est différent. Eh bien c’est la même chose !

Si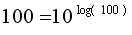

Alors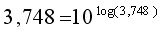

Et comment fait-on pour trouver le log de 3,748 ? On prend …… une calculatrice !

Autrement dit: log (3,748) = 0,574

Au passage on peut vérifier que si 3,748 = 3748 /1000 alors

log (3,748) = log (3748) – log (1000)

= log (3748) – 3 = 3,574 – 3 = 0,574

… et faire un tas d’autres exercices pour vérifier que l’on a bien compris, mais pour manipuler les décibels toutes ces notions sont suffisantes.

Share !