Mise en oeuvre de la Belton brick d’Accutronics

Les modules BTDR-1 , 2 et 3 produits par Accutronics sont des unités de réverbération numériques de taille adaptée au montage de pédales ou assez facilement intégrables en entrée d’un amplificateur.
Leur fonctionnement interne est relativement compliqué et la documentation sur les composants relativement succincte. Cela dit il est facile de les mettre en oeuvre si l’on a bien repéré les points à prendre en compte dans la documentation. C’est l’objet de cet article qui se propose d’étudier en particulier le circuit d’application conseillé par le constructeur. Si certains aspects vous semblent ici traités en mode survol , ne vous inquiétez pas, vous pourrez trouver les détails dans les documents (PDF et liens) cités en fin d’article avec quelques commentaires.
Les boitiers renferment 3 modules identiques montés en série : les unités de ligne à retard PT2399. Ce circuit , le PT2399 made in Taïwan, est très prisé des amateurs de DIY audio ( pour Merlin Blencowe, le « Valvewizard », c’est carrément un don de Dieu !).
Comme on le disait plus haut, le schéma du constructeur n’est pas explicite.
Sur la figure ci-dessous, nous voyons en pins 16 à 13 les entrées sorties des filtres passe-bas (Low Pass Filters) accessibles à l’utilisateur et en 12 à 9 les entrées sorties d’amplis opérationnels utilisés principalement comme intégrateurs dans les boucles de conversions analogique-numérique et inversement. Le retard est programmé par l’utilisateur par le choix de la résistance externe câblée en pin 6. Le constructeur fournit une table de correspondances retard <-> valeur de R dans la datasheet.
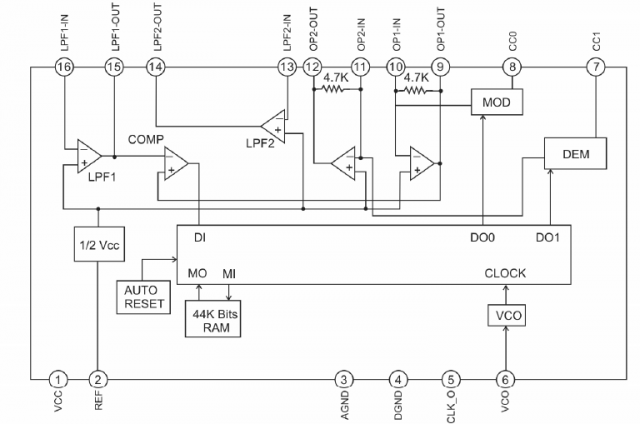
Schéma de principe du PT2399
Application simple du PT2399 :
Une application simple du PT2399 est la chambre d’écho dont le principe est le suivant :
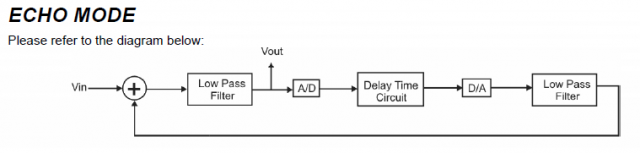
Le signal d’entrée Vin est filtré pour couper les fréquences supérieures, celles-ci ne se prêtant pas à l’écho, au délai ou à la réverbération.
Il est ensuite converti d’analogique à numérique ( A-> D) . Cette conversion s’opère par suréchantillonnage. C’est ici que réside la qualité du circuit, dans la conversion d’analogique à numérique. Ceux qui ont connaissance du principe selon lequel il est nécessaire d’échantillonner un signal à une fréquence au moins double de la fréquence la plus élevée contenue dans ce signal ( le célèbre théorème de Shannon) connaissent aussi les problèmes de rapport signal sur bruit que cela peut poser. Ici le système A/D est plus performant en procédant par suréchantillonnage , c’est-à-dire en utilisant une fréquence d’échantillonnage beaucoup plus élevée:
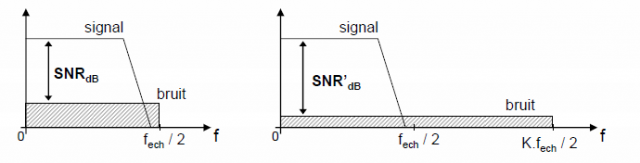
Les deux schémas ci-dessus sont des représentations spectrales du signal et du bruit , c’est-à-dire fréquences en abscisse et niveau en ordonnée. SNR = Signal to Noise Ratio = rapport signal sur bruit. Le bruit dont on parle ici est celui produit par la conversion : c’est le bruit de quantification et non le bruit thermique ou électro-magnétique propre à tout circuit électronique. Pour le distinguer on le note plutôt SQNR.
Le mode de conversion adopté dans le PT2399 dit Sigma-Delta permet d’augmenter considérablement le rapport SQNR en étalant la puissance de bruit jusqu’à la fréquence d’échantillonnage égale à K x fech/2. Le principe est ensuite de filtrer la bande utile du signal limitée à fech/2.
fech/2 est la fréquence maximale du signal à conserver, fech étant le double et correspondant au théorème de Shannon cité plus haut.
La cellule A/D du PT2399 est en fait une petite boucle d’asservissement dont le rôle est de poursuivre le signal d’entrée au plus près de sa valeur tout en produisant une image logique à deux niveaux 0 et 1 de cette poursuite !
Intuitivement si on se réfère au schéma suivant :
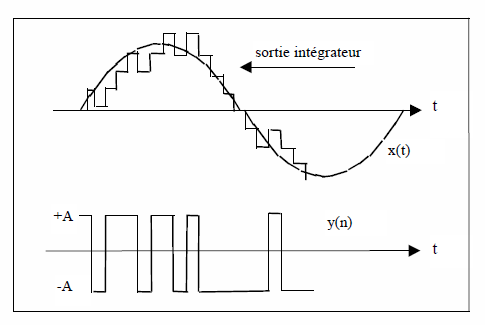
On voit que si l’on augmente la fréquence d’échantillonnage on colle davantage au signal d’entrée pour obtenir moins de distortion et moins de bruit de quantification SQNR. Les deux aspects, distortion et bruit de quantification sont en proportion directe. Pour donner l’exemple extrême , le PT2399 donne un délai de 30 ms pour une fréquence d’échantillonnage de 22 MHz ! Par rapport à un échantillonnage à 44,100 Hz le facteur K = 22e6 / 44100 = 499 et l’amélioration du SQNR est de 10 log(K) = 27 dB !
Le signal numérique est donc codé sur un seul bit pour rentrer dans le module delay time circuit . Ici en principe le signal est mémorisé et ressorti sous la même forme au terme du délai programmé.
C’est un simple filtre passe-bas (intégrateur) qui restitue le signal analogique. Ensuite le signal passe encore dans un passe-bas avant d’être sommé avec le signal d’entrée dans la boucle de feedback.
Intégration dans la Belton brick :
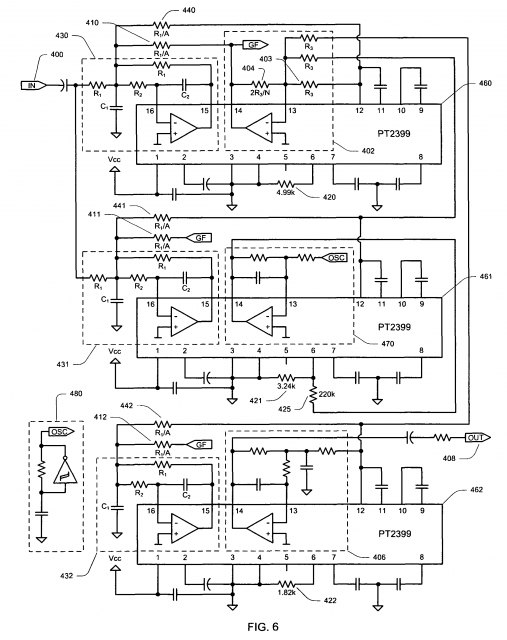
Ici l’on voit les 3 circuits mis en série avec divers rebouclages en multi-feedback avec sommations sur les entrées . On devine que cette conception s’est faite de manière plutôt empirique . D’après la datasheet les fréquences d’échantillonnage et donc les délais élémentaires générés sont dans l’ordre approximativement :
- 8 Mhz -> 86 ms
- 10 Mhz -> 68 ms
- 13 Mhz -> 52 ms
Un oscillateur basse fréquence a été superposé au circuit n°2 qui doit ajouter une sorte de chorus ou d’effet vintage au son mais réservé aux oreilles fines.
C’est la combinaison de ces trois montages qui simule un effet de réverbération. On constate également dans cette chaîne que la lutte contre le bruit doit être une priorité ! Avec ses 3 conversions A/D et surtout les multiples rebouclages le circuit ne demande qu’à produire du bruit soit de quantification, néanmoins maîtrisé, mais aussi thermique et électromagnétique.
Mise en œuvre :
Il faut bien entendu prêter attention à l’alimentation ainsi qu’aux caractéristiques d’entrée :
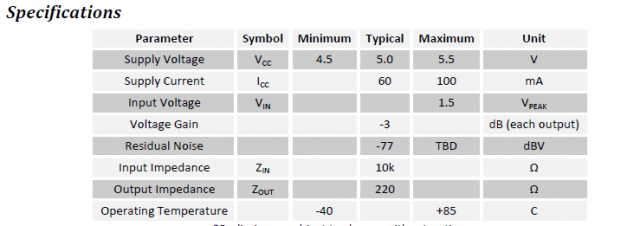
L’alimentation se fait sous 5 V /100 mA régulés et filtrés.
Les caractéristiques d’entrée sont : 1,5 V crête et Ze = 10 k. Autrement dit il est exclu d’y brancher directement un micro guitare. L’impédance d’entrée nécessite un buffer.
Le signal admissible crête à crête est de 2 x 1,5 = 3 V. Même si les convertisseurs intégrés sont de bonne qualité il est toujours préférable de présenter en entrée un signal dont l’amplitude s’approche du maximum ; c’est ainsi que l’on garantit le meilleur rapport Signal/bruit. Les signaux de nos micros guitare faisant au grand maximum 1 vcc d’amplitude à l’attaque de la corde grave , il n’est pas aberrant de mettre en entrée un ampli/buffer avec un gain de 3, d’autant que :
- si du clipping se fait entendre on peut baisser légèrement le volume sur la guitare.
- nous allons mettre devant, comme nous allons voir, un filtre passe-haut destiné à rejeter les fréquences basses qui présentent justement les niveaux les plus élevés.
Circuits d’application :
1. Avec la BTDR-1 :
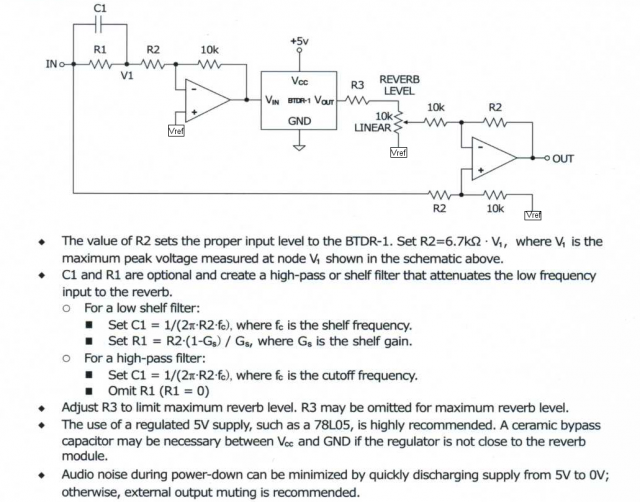
Voici le schéma théorique qui semble le plus approprié à la situation . La valeur de R2 détermine le niveau d’entrée qui convient pour la BTDR-1 , dit le texte. Il faut interpréter « qui convient pour assurer le meilleur rapport SNR possible ».
Fixer R2 = 6.7 k x V1 avec V1 = max Vc mesuré au noeud V1 sur le schéma ci-dessus. En guitare il est préférable de couper franchement les basses devant une réverbération et donc d’opter pour un filtre passe-haut pur en entrée. On n’utilisera donc pas R1 (il y a une erreur dans le texte : omit R1 => R1 infinie et non nulle.). Si nous reprenons Ve = 1,5 Vc, avec un gain de 3 nous aurons V1 = 0,5 Vc et donc R2 = 6,7 x 0.5 = 3.3 k. (Notons que cette valeur donnée 6,7 est liée au choix de la résistance de 10k pour assurer le gain 6,7 = 10K / 1,5 Vc)
Pour le filtre passe-haut :
\(C1 = \frac{1}{2\pi.3300 .fc}\)
- pour fc = 300 Hz C1 = 150 nF
- pour fc = 600 Hz C1 = 82 nF
- pour fc = 1000 Hz C1 = 47 nF
- etc….
Nul besoin de capacité d’entrée ou de sortie sur le circuit BTDR, elles sont intégrées comme on peut le voir plus haut : 4.7 µF en entrée et 10 µF en sortie.
On peut omettre R3 sauf si l’on a effectivement trop de signal en sortie. Nous verrons des variantes plus loin.
Le circuit suivant (de sortie) est un classique du montage à amplificateur opérationnel (AOP) . C’est un additionneur pondéré mais comme l’une des deux tensions est inversée , c’est en fait un soustracteur pondéré.
Pour bien mettre au point nos montages et aussi comprendre les schémas d’application existants, il est très utile de comprendre comment ce circuit fonctionne. Nous allons détailler en commençant par rappeler que l’AOP est l’un des circuits électroniques les plus simples qui soit quand on peut se contenter comme ici des caractéristiques de l’AOP idéal, soit :
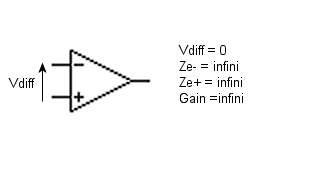
La tension entre les deux entrées est toujours nulle ainsi que les deux courants d’entrée. Le gain est considéré comme infini. Ces caractéristiques conviennent en particulier très bien à la famille des AOP à FET que nous utilisons, les TL07x , par exemple.
Sur la figure ci-dessous est représenté le cas général. On applique pour trouver Vs = f(V1,V2) la règle selon laquelle lorsqu’une tension de sortie dépend de n tensions d’entrée indépendantes, la tension de sortie est la somme des tensions résultant des n tensions d’entrée prises une à une avec les n-1 autres tensions ramenées à la masse.
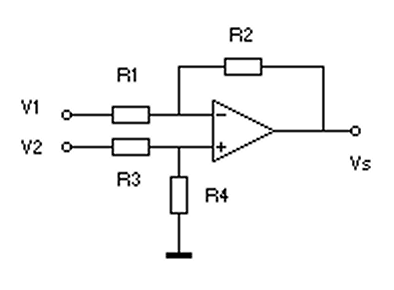
Autrement dit dans le cas qui nous occupe nous calculons Vs avec V2 = 0 (R3 à la masse donc) puis Vs avec V1 = 0 (R1 à la masse ) et on ajoute les deux expressions de Vs obtenues !
1. V2 = 0.
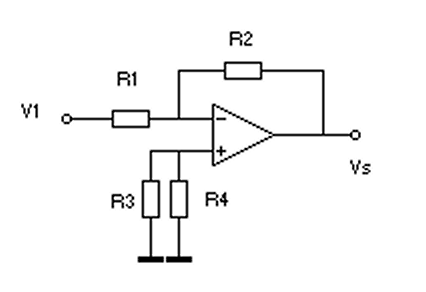
V2 étant nulle , R3 est ramenée à la masse en parallèle sur R4. Et le courant étant nul dans ces résistances , la tension aussi et l’entrée + est ramenée à la masse. Voir la figure suivante en bas à gauche :
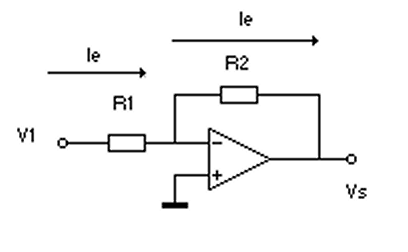
L’entrée + étant à la masse , l’entrée – aussi puisque Vdiff = 0. Comme le courant entrant en – est nul , le courant d’entrée Ie traversant R1 traverse aussi R2.On obtient:
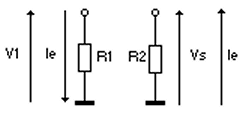
Il suffit d’écrire Ie = Ie et on obtient :
\(\frac{V1}{R1}=-\frac{Vs}{R2}\)
d’où :
\(Vs = -V1\frac{R2}{R1}\)
2. V1 = 0
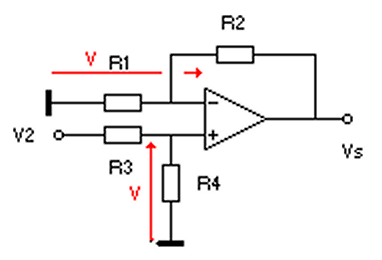
Ici c’est R1 qui est à la masse. Comme la tension entre + et – est nulle, c’est la même tension V que l’on trouve sur R4 et R1 d’où :
\(V =V2 \frac{R4}{R3+R4}\)
Le courant traversant R2 est le même que celui traversant R1 (puisque rien n’entre ni ne sort de l’entrée -) et ce courant vaut V / R1 . V étant maintenant connu en fonction de V2 , le problème est résolu.
\(\frac{Vs}{R2+R1}=\frac{V}{R1}\)
\(Vs\frac{R1}{R2+R1}=V=V2 \frac{R4}{R3+R4}\)
\(Vs=V2\frac{R1+R2}{R1} \frac{R4}{R3+R4}\)
3. Résultat
\(Vs = -V1\frac{R2}{R1}+V2\frac{R1+R2}{R1} \frac{R4}{R3+R4}\)
Si nous reprenons le schéma de sortie du montage BTDR :
- R1 = R4 = 10k
- R3 = R2
- V1 = Vr (tension réverbérée prise au curseur du potentiomètre)
- V2 = Vin
nous pouvons écrire :
\(Vs = -Vr\frac{R2}{10k}+Vin\frac{10k+R2}{10k} \frac{10k}{R2+10k}\)
autrement dit
\(Vs =Vin -Vr\frac{R2}{10k}\)
mais comme le buffer d’entrée amplifie en inversant la tension il faut inverser le signe du signal réverbéré et on obtient :
\(Vs =Vin +Vr\alpha\)
avec
\( \alpha=\frac{R2}{10k} \)
soit l’inverse du gain de l’étage d’entrée. Nous avons choisi R2 = 3k3 et donc \( \alpha= \frac{1}{3}\).
Si le BTDR lui-même n’atténuait pas de 3 dB et avec le potentiomètre de sortie à fond nous aurions exactement
\(Vs =Vin +Vin reverbéré\)
du fait que le signal à réverbérer est amplifié du facteur \( \alpha\) en entrée pour être atténué du même facteur en sortie.
2 . Avec la BTDR-3
La BTDR-3 présente les mêmes caractéristiques que la BTDR-1 à l’exception d’un réglage supplémentaire de la profondeur de réverbération qui nécessite un potentiomètre double supplémentaire. Le brochage est également différent. Le constructeur propose un autre circuit d’application qui convient également au BTDR-1. C’est le schéma théorique suivant :
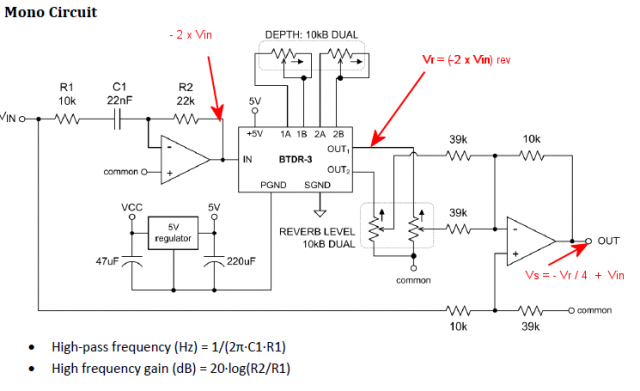
En entrée le filtre passe haut a un gain d’environ 2 avec R2/R1 = 2.2 dans la bande passante et sa fréquence de coupure est de
\( \frac{1}{2\Pi C1 R1}= \frac{1}{2\Pi.22e-9.10000} = 723 Hz \)
En sortie nous avons le même circuit additionneur vu plus haut. Les sorties stéréo ne changent rien : les tensions sur les deux résistances de 39 k en parallèle s’ajoutent et le raisonnement est le même. Nous pourrons raisonner sur une seule sortie
Si nous reprenons le résultat vu ici :
\(Vs = -V1\frac{R2}{R1}+V2\frac{R1+R2}{R1} \frac{R4}{R3+R4}\)
avec V1 = la tension réverbérée Vr et V2 la tension d’entrée Vin nous obtenons avec :
- R1 = R4 =39k
- R2 = R3 = 10k
\(Vs = -Vr\frac{R2}{R1}+Vin\frac{R1+R2}{R1} \frac{R4}{R3+R4}=-Vr\frac{R2}{R1}+Vin\frac{R1+R2}{R1} \frac{R1}{R2+R1}=-Vr\frac{R2}{R1}+Vin = -Vr\frac{10000}{39000}+Vin\)
d’où :
\(Vs = – \frac{Vr}{4} + Vin\)
Sachant que la tension qui entre dans la BTDR est -2 x Vin, \( – \frac{Vr}{4}= \frac{Vinrev}{2}\) avec Vinrev = Vin réverbérée , donc :
\(Vs = \frac{Vinrev}{2} + Vin\)
Par rapport au premier circuit d’application ( celui de la BTDR-1) , le constructeur a choisi de diviser par deux la tension réverbérée. Il semble donc qu’un rapport de 2 entre l’entrée et la sortie soit le plus efficace.
Application pratique : la pédale de Neunaber Technology :
(Cliquer pour agrandir)
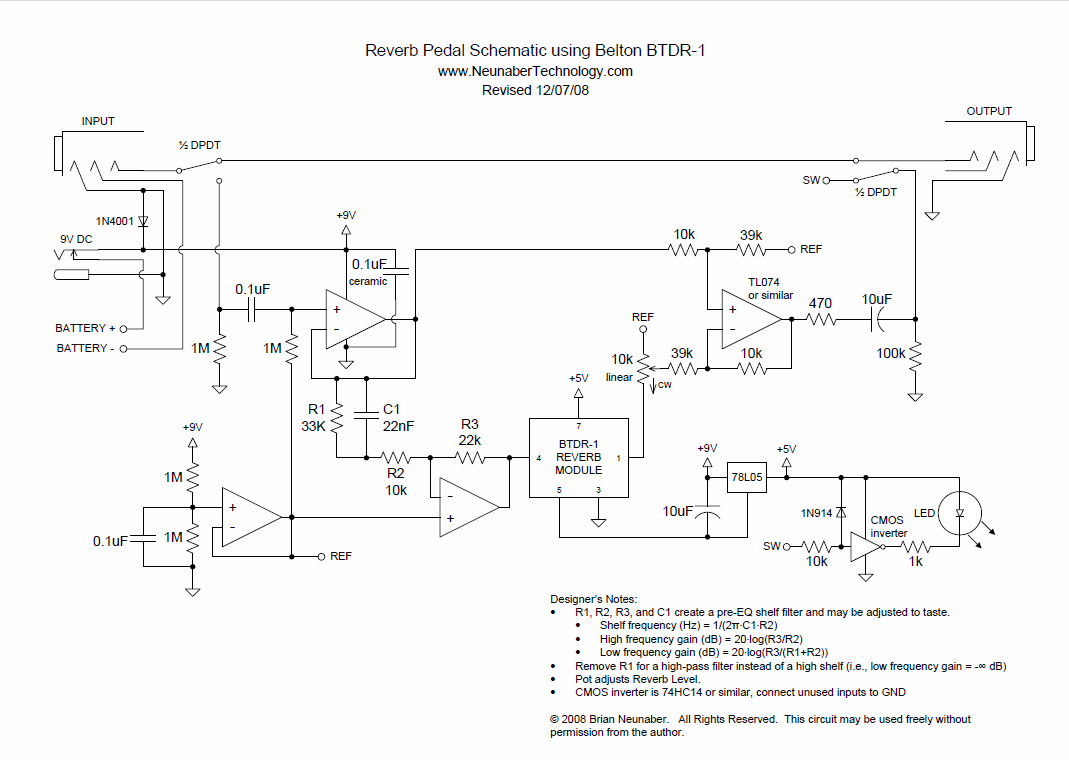
On voit qu’il s’agit de la stricte application pour la BTDR-1 du circuit proposé par le fabricant pour la BTDR-3 (peut-être même Accutronics/Belton a-t’il proposé le schéma de Neunaber) . Le TL074 (QuadAOP) peut être remplacé par 4 TL071 ou 2 TL072.
Le premier ampli op est un buffer, nécessaire car l’inverseur qui attaque la BTDR n’a que 10k d’impédance d’entrée et ne peut charger un micro guitare.
Le circuit en bas à gauche est un suiveur destiné à fournir le 0V de référence pour les AOP qui travaillent en symétrique. Ce « 0v » est ici au potentiel de 4.5 v , le système étant alimenté en 9v (bien qu’une batterie puisse sembler légère pour alimenter la BTDR).
Application avec un gain de 3 en entrée de la BTDR :
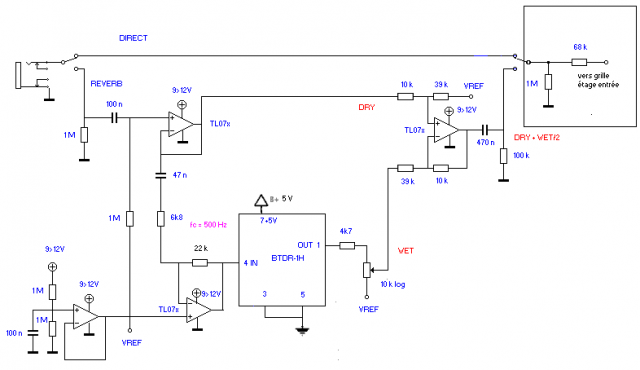
Le gain a été porté à 3 par la résistance de 6k8 en lieu et place de la 10 k. Le signal en sortie OUT doit alors être divisé par 6. Le signal wet est les 2/3 de OUT avec le potentiomètre à fond. Il est divisé par 4 par le sommateur , ce qui donne OUT/6.
Ce schéma est destiné à l’entrée d’un ampli. Le signal dry + wet/2 est envoyé sur la grille d’entrée à la place du signal du micro guitare.
(à l’étude : une BTDR pilotée par tube….)
Références :
- Ci-dessous quelques références sur la théorie de la conversion analogique-numérique et inversement, ne serait-ce que pour mieux comprendre la conversion sigma-delta utilisée dans le PT2399 et donc dans la Belton brick.
- Quelques éclaircissements sur le circuit PT2399 :


