Le théorème de Miller
Enoncé – Démonstration – Applications
Ce théorème est plus facile à démontrer et à utiliser qu’à énoncer :
Enoncé :
Soit un quadripôle amplificateur de gain A (A est supérieur ou égal à 1 en valeur absolue). Une impédance Z reliant l’entrée à la sortie est équivalente à deux impédances , l’une , Z1, en parallèle sur l’entrée valant Z / ( 1-A) , l’autre Z2 en parallèle sur la sortie valant A.Z / (A -1). Ce phénomène est également connu sous le nom d’effet Miller.
Démonstration :
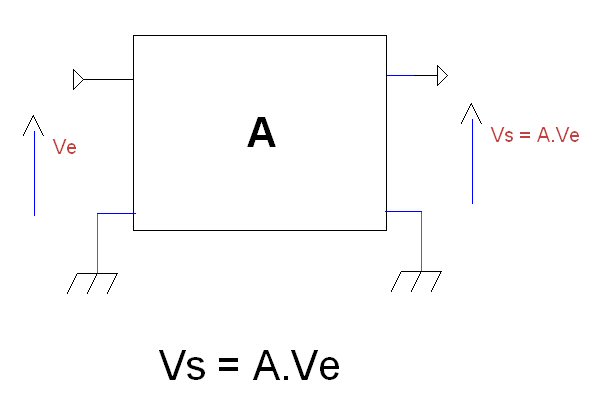
Voici le quadripôle amplificateur de gain A en question ( fonction de transfert = A). . Nous avons Vs = A.Ve ( On désigne aussi ce quadripôle comme un circuit linéaire car Vs est une fonction linéaire de Ve).
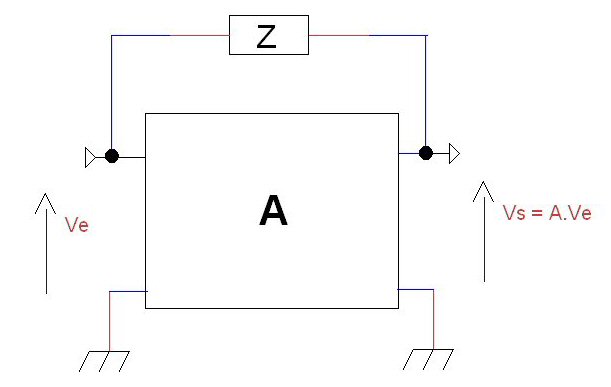
Nous amenons une impédance Z en parallèle au quadripôle reliant l’entrée à la sortie :
En nous référant à la loi d’ohm (sans oublier la règle du signe – voir fig.2) nous pouvons dire que l’impédance Z est traversée par un courant i sous une tension qui vaut Ve – Vs : pour être plus précis le potentiel en entrée étant Ve et celui en sortie Vs , la différence de potentiel entrée/sortie vaut Ve – Vs = Ve – A.Ve = Ve (1-A).
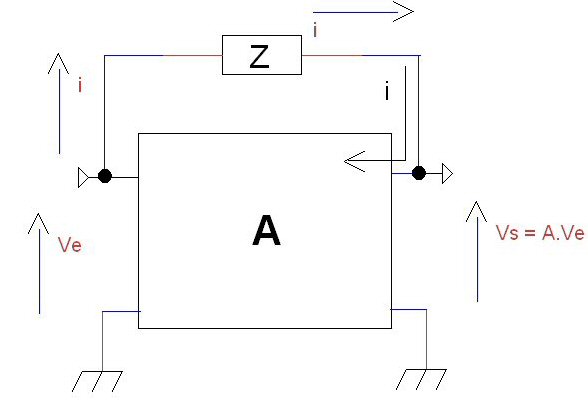
Connaissant Z et la tension sur Z je peux calculer i :
\(i = \frac {V_e – V_s}{Z}\)
\(i = \frac {V_e – A V_e}{Z} =\frac{V_e (1-A)}{Z}\)
Ce courant supplémentaire i imposé sur l’entrée par la présence de Z est prélevé sur le générateur qui applique Ve. Ce générateur voit l’impédance Z de la même manière qu’il verrait une impédance Z1 en parallèle sur l’entrée consommant le même courant i
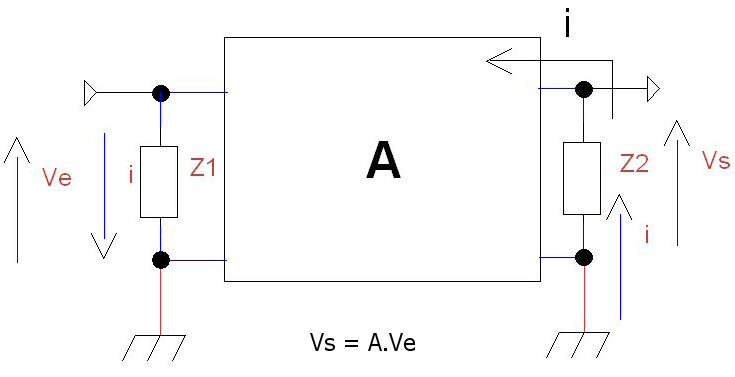
Que vaut Z1 ? En application directe de la loi d’ohm :
\(Z_1 = \frac{V_e}{i} = \frac{V_e}{Ve \frac{1-A}{Z}} = \frac{Z}{1-A}\)
Pour calculer Z2 nous considérons i entrant dans le quadripôle par la sortie et toujours en application directe de la loi d’ohm :
\(Z_2 = \frac{-V_s}{i} = \frac{-A V_e}{Ve \frac{1-A}{Z}} = \frac{-A Z}{1-A} = \frac{A Z}{A-1} \)
…ce qu’il fallait démontrer
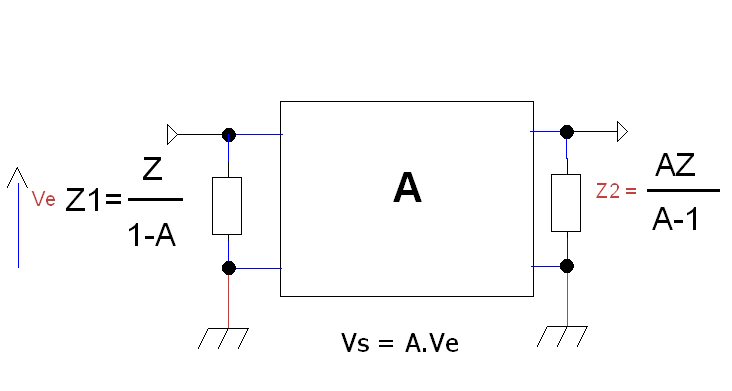
Ce théorème est appliqué sur un étage amplificateur inverseur , donc A est négatif et grand devant 1 . On fait alors l’approximation Z1 =~ Z / A et Z2 =~ Z. On dit alors que l’impédance sur l’entrée est l‘impédance Z divisée par le gain A. L’impédance sur la sortie est égale à Z.
Attention : Nous ne ferons l’utilisation de ce théorème que dans les deux applications qui suivent. Il est conseillé de ne pas l’utiliser autrement : tout abus du théorème de Miller peut nuire gravement au raisonnement !
Applications :
Les 2 applications que nous utiliserons sont systématiques dans tous les amplificateurs :
|
1. Montage en amplificateur : A >> 1:
Nous prenons le cas bien réel d’un étage amplificateur représenté ci-dessous par le rectangle et son gain A ( nous verrons plus tard qu’il s’agit d’une triode montée en cathode commune et tous ces termes seront explicités) . Dans ce montage , ce gain en tension A est négatif et sa valeur absolue est grande devant 1 .
Il faut écrire |A| >> 1 . Supposons A = -40.
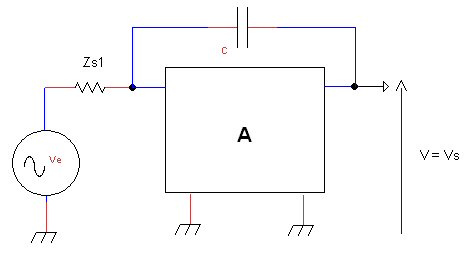
Nous allons évaluer l’incidence d’une capacité parasite C (elle aussi bien réelle) qui boucle l’entrée de l’ampli avec la sortie. Nous considérons également l’étage précédent représenté ci-dessus par un générateur de Thévenin dont la tension est Ve , supposée être la tension d’entrée de A, et dont l’impédance de sortie est Zs1.
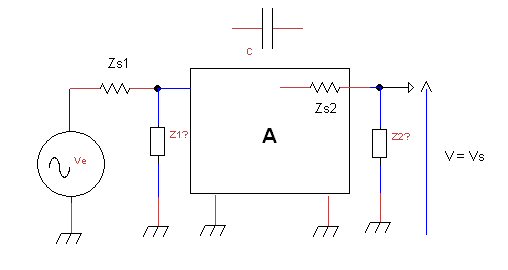
L’impédance Zc de la capacité C est celle appelée Z dans l’énoncé du théorème de Miller. A étant grand devant 1 on peut faire les approximations vues ci-dessus :
\(Z_1 = \frac {Z_c}{A}\)
et
\(Z_2 = Z_c\)
On en déduit :
\(Z_1 = \frac {\frac{1}{jC\omega}}{A}=\frac{1}{jAC\omega}\)
et
\(Z_2 = Z_c =\frac{1}{jC\omega}\)
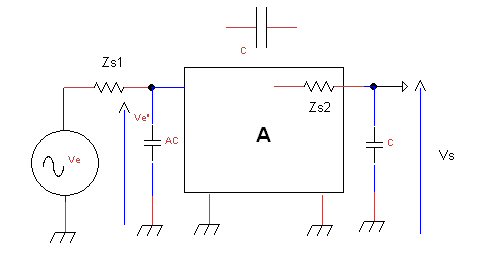
Tout se passe donc comme si la capacité C était multipliée par le gain A avant de se retrouver en parallèle sur l’entrée de l’amplificateur puisque Z1 = 1 / jACw. On parle alors de l’effet Miller . On appelle aussi parfois la capacité résultante AxC la capacité de Miller. On constate aussi que la capacité C se retrouve en outre intégralement sur la sortie ( Z2 = impédance de C).
Ce phénomène limite en principe la bande passante de l’amplificateur car on voit se profiler sur le schéma ci-dessus deux filtres passe-bas l’un en entrée dont la fréquence de coupure est 1 / 2 Pi A.C.Zs1, l’autre en sortie dont la fréquence de coupure est 1 / 2 Pi Zs2.C. (si ces notions sont obscures il est impératif de revoir le chapitre sur les filtres )
Exemple numérique :
Zs1 = 100 Ko
A = 40 soit ….. dB ( calculer de tête ! – sinon revoir l’article : une unité pratique : le décibel )
C = 1,6 pF ( capacité parasite de la 12AX7)
AC = 40 x 1,6 pF = 64 pF
Fc = 1 / 2 x 3,1416 x 64e-12 x 100 000 = 24 900 Hz
La fréquence de coupure est ici au-dessus de la bande audio ( 20 kHz) car nous avons choisi un gain raisonnable de 40 et l’impédance de sortie Zs1 est également raisonnable : avec un gain A de 100 et Zs1 = 200 ko, la fréquence de coupure tombe en -dessous de 5 kHz, donc prudence dans les calculs de conception !
En sortie il est rare que les valeurs soient critiques : si Zs2 = 100 ko (c’est souvent moins)
fc = 1 / 2 x 3,1416 x 1,6e-12 x 100 000 = 99 500 Hz ( c’est sans conséquence en audio et la marge est grande).
Attention néanmoins :Dans le raisonnement ci-dessus on a considéré que l’impédance d’entrée de l’amplificateur était grande devant Zs1 , ce qui est le cas en règle générale. Si ce n’est pas la cas il faut la prendre en compte : appelons la Ze2.
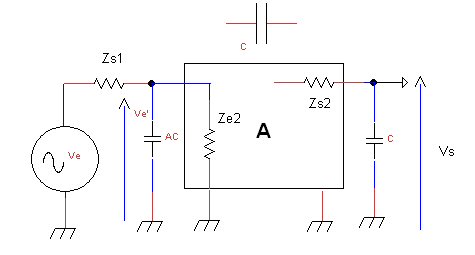
On voit sur le schéma ci-dessus que nous trouvons avec Ze2 et Zs1 un diviseur de tension sur Ve. Laissons de côté pour le moment la capacité de Miller ( AC) et cherchons quel est le générateur de Thévenin constitué par Ve, Zs1 et Zs2 :
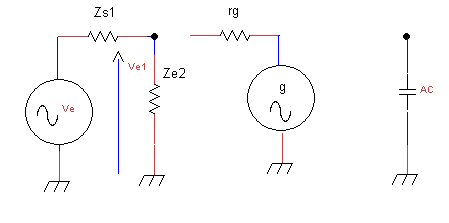
Avant de connecter le générateur g qui nous permettra de mesurer l’impédance de sortie , nous voyons que la tension de Thévenin du générateur est maintenant :
\(V_e1 = V_e \frac{Z_e2}{Z_e2 + Z_s1}\)
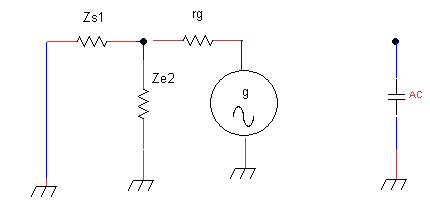
Pour mesurer l’impédance de sortie, nous connectons le générateur g en sortie en court-circuitant le générateur en entrée comme vu lors de l‘exposé de la méthode
Nous voyons que la nouvelle impédance de sortie est Zs1 // Ze2
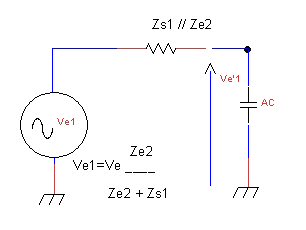
La figure ci-dessus représente le générateur de Thévenin obtenu attaquant la capacité de Miller AC. La fréquence de coupure devient maintenant :
\(f_c= \frac {1}{2 \pi (Z_s1//Z_e2) AC}\)
Conclusion : La prise en compte de Ze2 implique que la tension maintenant à l’entrée de l’amplificateur est atténuée mais que la fréquence de coupure du passe-bas en entrée est légèrement plus élevée du fait de la diminution de l’impédance de sortie.
2. Montage en adaptateur d’impédance : A = 1
Cette fois nous utilisons le quadripôle en adaptateur d’impédance. Son utilité est de s’interposer entre deux étages afin de réduire l’effet de l’impédance de sortie de l’étage précédent .Ses caractéristiques sont :
- Une impédance d’entrée élevée
- Une impédance de sortie faible : moins d’un kilohm
- un gain de 1 . A = 1. C’est-à-dire qu’en fait il n’y a pas de gain.
(Nous verrons plus loin qu’il s’agit d’un montage à triode que l’on appelle indifféremment à anode commune ou à cathode suiveuse)
Ce montage présente physiquement également une capacité parasite entre l’entrée et la sortie. Mais quelle est son influence ?

Avec A = 1 , nous voyons que VS = Ve et que Z1 et Z2 valent l’infini (= Z/0) ! Et une impédance infinie est une impédance qui n’existe pas !
Tout s’explique si nous reprenons notre schéma d’origine :

Avec A = 1 , Vs = Ve et la tension sur Z est nulle ainsi que le courant i. La capacité parasite n’a donc pas d’influence si A = 1.
Il n’y a donc aucun effet Miller sur un montage adaptateur d’impédance.
Comment se sert-on de ce montage ? Nous allons comprendre son utilité en reprenant notre montage amplificateur précédent ( A >> 1) victime de l’effet Miller :
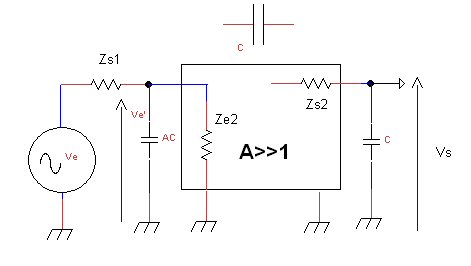
Rappelons que Ze2 est une impédance d’entrée à prendre en compte devant Zs1, impédance de sortie de l’étage précédent. Nous avons vu que Zs1, Ze2 et AC ne faisaient pas bon ménage car outre que nous avons un diviseur de tension , nous avons aussi un filtre passe-bas.
Intercalons donc un adaptateur d’impédance :
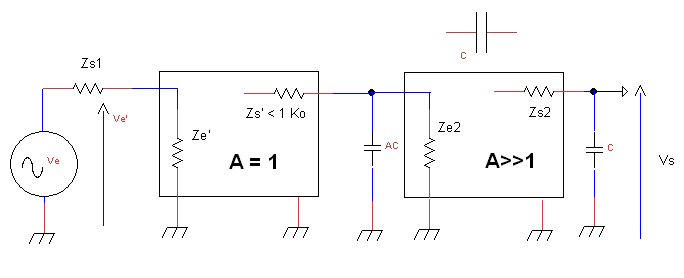
Au bilan nous voyons que :
- En choisissant Ze’ grand devant Zs1 , nous avons éliminé l’influence de cette dernière en tant que diviseur de tension avec Ze2 avant modification.
- Comme il n’y a pas d’effet Miller sur l’adaptateur, il n’y a plus de filtre passe-bas avec Zs1 non plus.
- Comme Zs’ est très faible ( environ 500 ohms ) , il n’y a plus ni diviseur de tension (ou négligeable) avec Ze2 , ni de filtre passe-bas car Zs’ // Ze2 =~ Zs’ et le passe-bas formé entre Zs’ et AC voit sa fréquence de coupure rejetée très haut.
Si l’on reprend l’exemple numérique ci-dessus on voit que nous avons 500 ohms à la place de Zs1 = 100 kohms. La fréquence de coupure fc est multipliée par 100000 / 500 = 200 ! Nous avons donc également supprimé l’effet Miller sur le second étage dont on peut alors augmenter considérablement le gain en conservant toute la bande passante audio.
On comprend ainsi l’usage très précieux que l’on peut faire d’un adaptateur d’impédance conçu comme un réducteur d’impédance.
Copyright ProjetG5 – Rédacteur jptrol
mis à jour le 17 juin 2007


