CULTIVONS NOS DIFFERENTIELLES
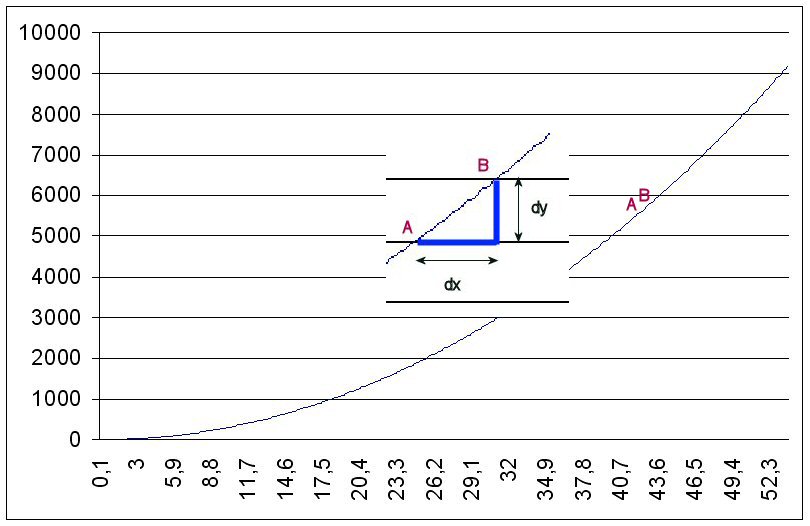
Soit une fonction quelconque y = f(x) représentée par la courbe ci-dessous .
Si l’on prend deux points A et B sur la courbe avec B proche de A on peut dire que la différentielle au point A est la quantité dy / dx .
C’est la pente de la droite (D) qui passe par A et B.
Voilà c’est tout mais……..
DERIVER C’EST PRENDRE LA TANGENTE
*********************************************
numérique est égale à la pente de ladroite . On associe donc à une fonction
y = f(x) une autre fonction y’ = f'(x) qui associe à chaque point (x,y) une valeur y’ = pente de la tangente à ce point.
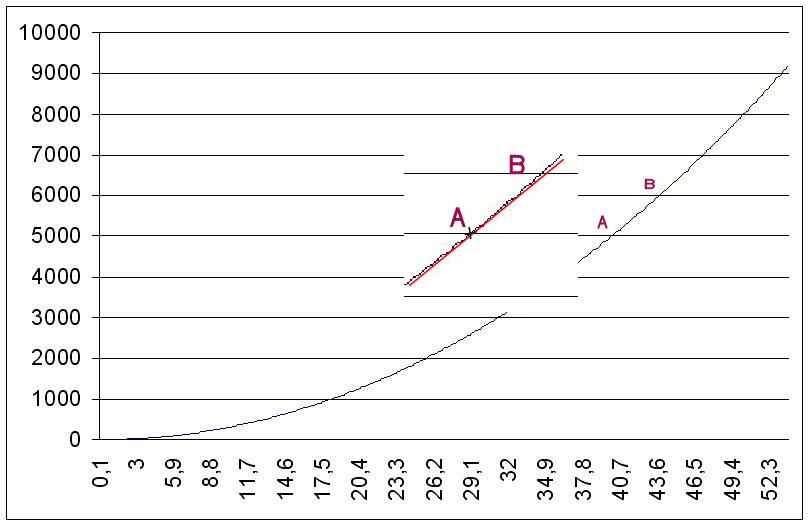
La courbe est ici une droite de pente a. Il est évident que tous les points de cette droite ont la même droite comme tangente et que y’ = a.
2 ème cas y = sin x
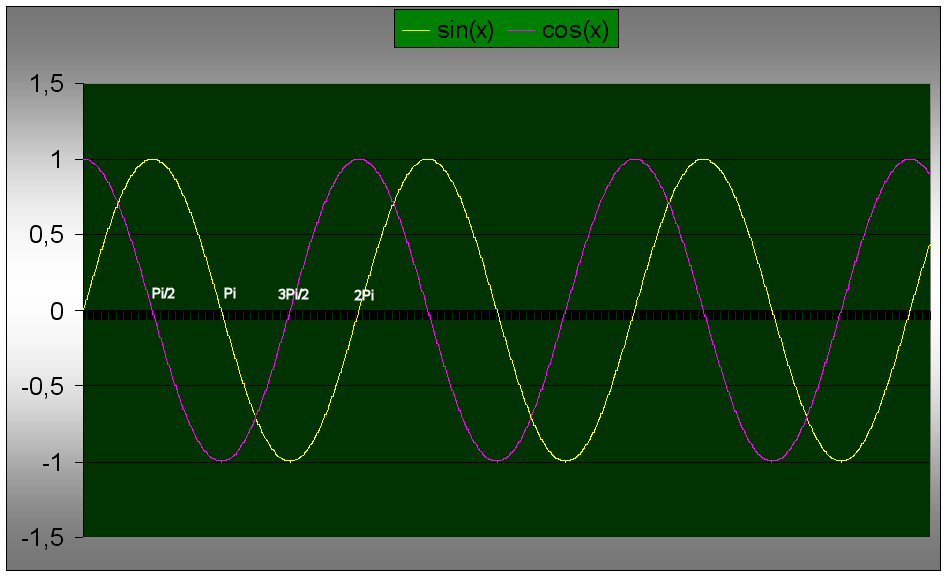
Si l’on observe que la pente de la tangente en Pi/2 est nulle on voit que c’est aussi la valeur de cos x au même point.
La pente de la tangente de la courbe jaune est à nouveau maximum en Pi mais dans l’autre sens ( dy/dx < 0 car dy <0 ) : elle vaut -1 comme la valeur du cosinus au même point.
La pente de la tangente de la courbe jaune s’annule à nouveau en 3Pi/2. C’est encore
la valeur du cosinus ( cos 3Pi/2 = 0 ). On retrouve la pente de 1 en x = 2Pi qui correspond à cos 2Pi.
Bref comme on le constate la dérivée de sin x c’est cos x.
sin ‘ x = cos x
D’autre part nous avons vu que sin ( x + Pi/2) = cos x
Donc
Une dernière notion sur les dérivées pour bien comprendre les rapports courants/tensions dans les impédances complexes que sont les selfs et les capacités :
Que vaut alors la dérivée de Y par rapport à t ?
Il suffit de retourner à nos différentielles : Y’ = limite de dY/dt quand dt tend vers 0 .
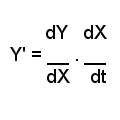
On voit ici que la dérivée est égale au produit des deux dérivées. Donc si Y = sin X et X = a t alors Y = sin (a t) et Y’ = cos (a t) x a
d’où en conclusion :
=> Y’ = a sin (at + Pi/2)
Cette formule est fondamentale pour bien comprendre les rapports courants/tensions dans les impédances complexes que sont les selfs et les capacités d’autant que tous les signaux , même les plus complexes, sont composés d’une multitude de simples signaux sinusoïdaux superposés.


