1.4 Bande passante - Le décibel

CHAPITRE 1 : 1.4

Notion de bande passante– Une unité pratique : le décibel

Notion de bande passante

Dans le domaine de l’audio les fréquences audibles s’étalent d’environ 16 Hz à 20 000 Hz.

Prenons l’exemple d’un amplificateur HI-FI. Celui-ci se doit d’amplifier fidèlement chaque fréquence présente dans le signal d’entrée . On définit comme étant dans la bande passante de l’amplificateur de puissance P toutes les fréquences que l’amplificateur est capable de délivrer (fidèlement c’est-dire ici sans distortion) avec une puissance comprise entre P/2 et P pour un même niveau nominal d’entrée. (Il va de soi que ces caractéristiques ne peuvent être mesurées qu’avec un générateur de fréquence).

Ainsi pour un ampli HI-FI de 60 W on mesure la puissance de sortie en appliquant un signal de 775 mVeff (valeur normalisée voir ci-dessous ) en entrée : pour que la fréquence choisie soit dans la bande passante il faut et il suffit que la puissance en sortie soit comprise entre 30 W et 60 W.

On étend cette notion à tout quadripôle . C’est ainsi que l’on nomme tout dispositif à l’entrée duquel on peut appliquer une tension , traitée par lui, et recueillir en sortie un tension résultante. Nous connaissions les dipôles avec les résistances, les capacités et les selfs.

Les quadripôles que nous allons étudier sont des amplificateurs complets, des étages d’amplification, des filtres etc … revoir éventuellement la conclusion sur le théorème de Thevenin

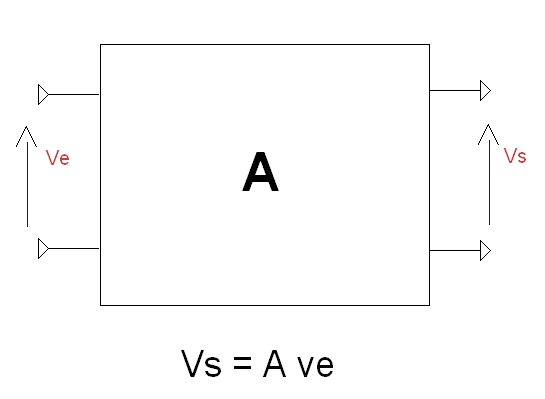
La fonction A peut être l’amplification ou le gain pour un étage amplificateur ou l‘atténuation pour un filtre ou un étage de couplage (voir plus loin) . Dans le cas d’un filtre ( et nous verrons que nous en rencontrons beaucoup dans nos amplificateurs ) on parle aussi de transmittance : Vs = f(Ve) = T(jw) Ve

Il n’est pas toujours pratique de savoir ce que représente la valeur nominale de Ve . Aussi parle -t’on de bande passante le plus souvent en se référant à une valeur connue de la tension de sortie Vs0 pour une fréquence f0 de référence connue pour être dans la bande passante et délivrant la puissance maximale nominale.

Une fois que j’ai chargé mon quadripôle avec une impédance ZL je sais que ma tension VS0 va délivrer une puissance

\(P = \frac {Vs0^2}{Z_L}\)

La question est maintenant à quelle condition ma fréquence f1 qui produit la puissance P1 sera-t’elle dans la bande passante . La condition est que :

\(P1 = \frac {Vs1^2}{Z_L} >= \frac {P0}{2}\)

…. en fait que P1 soit au moins égale à la moitié de P0.

Donc que :

\(\frac {Vs1^2}{Z_L} >= \frac {Vs0^2}{2 Z_L}\)

\( Vs1^2 >= \frac {Vs0^2}{2}\)

D’où : \(Vs1 >= \frac {Vs0}{1.414}\)

(1.414 = racine carrée de 2 )

Ainsi pour que l’on reste dans la bande passante il suffit que la tension de sortie ne chute pas de plus de 0.707 fois la tension de sortie de référence.

Il faut bien convenir que ces aspects de rapports de puissances et de tensions ne sont pas faciles à gérer : mais une unité pratique est utilisée permettant de simplifier ces problèmes : le décibel.

Une unité pratique : le décibel

Afin de bien comprendre le sujet il est nécessaire d’être familiarisé avec les logarithmes, mais rassurez-vous la simple lecture du chapitre de rappel ici suffit.

Comme il est dit dans ce chapitre l’utilisation des logarithmes permet de matérialiser les rapports de grandeurs plus ou moins disproportionnées . Ainsi à l’origine il avait été envisagé pour comparer deux puissances P1 et P2 de prendre le logarithme de leur rapport :

\( log \frac {P2}{P1}\)

L’unité utilisée aurait alors été le Bel ( de Graham Bell, l’inventeur du téléphone : on avait supprimé un l pour ne pas que ça fasse cloche en anglais). Ainsi un rapport de 2 ( P2 = 2 x P1) donnait 0,3 Bel ( calculatrice en mains !).

Pour être pratique à manipuler, l’unité retenue a en fait été divisée par 10 : c’est le décibel . Le rapport de 2 pour P2 = 2 x P1 devient 3 décibels ou 3 dB

Voici donc la formule fondamentale qui donne soit l’amplification de la puissance soit l’atténuation en dB:

\(A_d{_B} = 10 \ log\ \frac {P2}{P1}\)

Si la puissance P2 valait la moitié de P1 alors nous aurions une atténuation de :

\( 10 \log (0,5) = \quad – 3 dB\)

Ce qui est logique après tout.

On peut ainsi se construire mentalement un système de repérage des rapports de puissance assez facilement, et sans faire de calculs en sachant qu’à chaque fois que je double ma puissance j’ajoute 3 dB:

Rapport des puissances	dB
2	3
4	6
8	9
16	12
32	15

On peut ajouter à ce tableau des valeurs remarquables :

Ainsi puisque log (1) = 0 nous savons que le gain unitaire ( ou l’atténuation nulle ) avec P2 = P1 donne O dB.

Nous savons aussi que log (10) = 1 donc 10 log (10) = 10 dB et si P2 = 10 x P1 alors le rapport des puissances P2 / P1 est égal à 10 dB . On peut alors compléter le tableau ci-dessus :

Rapport des puissances	dB
1	0
2	3
4	6
8	9
10	10
16	12
20	13
32	15
40	16
64	18

Ci-dessus on lit par exemple que P2/P1 = 20 donc 10 x 2 donc 10 dB + 3 dB = 13 dB.

Pour une atténuation on prend le signe opposé : si l’on divise la puissance par 32 le rapport d’atténuation est de
– 15 dB.

Qu’en est-il maintenant des rapports de tensions ?

Nous savons que P2 = V2² / Z et P1 = V1² / Z. (revoir au besoin la démonstration )

Donc

\( \frac {P_2}{P_1} = \frac {V_2^2}{V_1^2}\)

De là il vient :

\( \frac {P_2}{P_1} = \frac {V_2^2}{V_1^2} = \left(\frac{V_2}{V_1}\right)^2 \Rightarrow log\frac{P_2}{P_1} = 2 \log \frac{V_2}{V_1} \Rightarrow 10\log\frac{P_2}{P_1} = 20 \log \frac{V_2}{V_1}\)

Le gain ou l’atténuation en tensions devient :

\(A_d{_B} = 20 \ log\ \frac {V2}{V1}\)

Ainsi la valeur en dB est la même que l’on raisonne en puissances ou en tensions.

On peut alors faire un tableau plus complet :

Rapport des puissances	Rapport des tensions	dB
1	1	0
2	1,414 (=racine de 2)	3
4	2	6
8	2,82 (=racine de 8)	9
10	3,16(=racine de 10)	10
16	4	12
20	4,47 (=racine de 20)	13
32	5.66	15
40	6.32	16
64	8	18
100	10	20

D’après ce que nous avons lu à l’article précédent sur la bande passante nous voyons que la limite de la bande passante est de – 3 dB.

D’autres valeurs remarquables sont : 6 dB pour un rapport de tensions de 2.

Ces notions sont indispensables pour comprendre les filtres et les bandes passantes des amplificateurs.

Pourquoi 0 dB = 775 mVeff ? : il s’agit d’une référence adoptée en téléphonie normalisée où les lignes cuivre présentent une impédance de 600 ohms. La tension de 775 mVeff représente 1 mW sur cette impédance.

Retour au sommaire général

Share !