Chapitre 3 : La triode (suite)

Montages en cathode commune ( amplificateur) :

Amplificateur à triode en cathode commune parfaitement découplée

• • Gain
  • Impédance d’entrée
  • Impédance de sortie
  • bande passante

 

Calcul du gain

(Schéma équivalent pour l’alternatif ci-dessous)

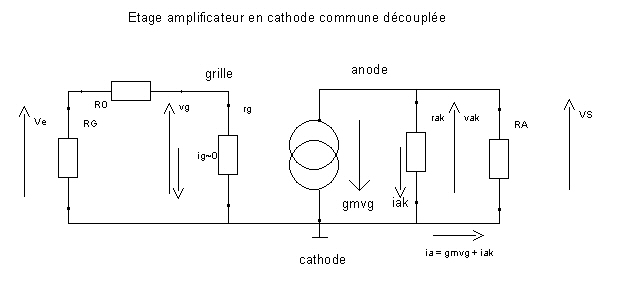
Avec :

• • • rak = résistance interne de la triode ( cf Datasheet)
    • VAK = tension anode – cathode
    • gm =transconductance ( cf Datasheet)
    • RA l’impédance de charge sur l’anode
    • rg = résistance de grille considérée comme très grande
    • ig = courant de grille considéré comme très faible et négligeable par rapport aux autres courants
    • R0 = résistance de protection de la grille ( grid-stopper)

La résistance Rk de cathode est considérée en court-circuit par la capacité Ck.
Le courant ig étant considéré comme nul traversant R0, il n’y a pas de tension aux bornes de R0 et donc

vg = Ve

Nous calculons le gain soit :

\(A = \frac {V_S}{V_e}= \frac {V_S}{V_g}\)

La résistance de charge RA est traversée par le courant ia = gmvg + iak dans le même sens que la tension VS,  la loi d’ohm    nous dit que VS = – RA ia ( attention au signe) soit :

\(V_S = -RA.(gmvg+iak) = – RA.(gmvg+\frac {vak}{rak})\)

mais VS = vak  et vg = Ve donc

\(V_S = -RA.(gmV_e+\frac{V_S}{rak}) \)

\(V_S +RA.\frac{V_S}{rak} = – RA.(gmV_e)\)

nous savons que d’autre part que gm . rak = µ donc gm = µ / rak  et

\(V_S.(1+\frac{RA}{rak}) =  – RA.\frac {µ}{rak}.V_e\)

\(\frac{V_S}{V_e}=-\frac{ \frac{µRA}{rak}}{\frac{rak+RA}{rak} } = – \frac {µRA}{rak+RA}\)

le gain A étant VS / Ve nous avons donc la formule du gain :

\(A = – \frac {µRA}{rak+RA}\)

Le signe – signifie que Ve et VS sont en opposition de phase.

On peut donc représenter l’étage par un générateur de Thévenin chargé par RA sachant maintenant que

\(V_S= – µV_e \frac {RA}{rak+RA}\)

 

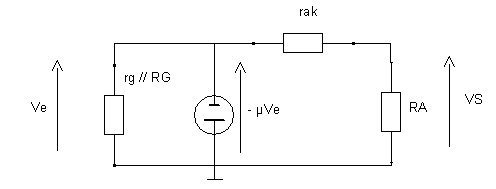
On a donc grandement simplifié le problème : on voit que Ve a simplement été multiplié par µ et que la tension -µVe résultante est appliquée sur un simple diviseur de tension pour obtenir VS

---

Calcul de l’impédance d’entrée

 

(Schéma équivalent pour l’alternatif)

Avec :

• • rak = résistance interne de la triode ( cf Datasheet)
  • VAK = tension anode – cathode
  • gm = transconductance ( cf Datasheet)
  • RA = l’impédance de charge sur l’anode
  • rg = résistance de grille considérée comme très grande
  • ig = courant de grille considéré comme très faible et négligeable par rapport aux autres courants
  • R0 = résistance de protection de la grille ( grid-stopper)
  • RG = résistance extérieure en entrée de l’étage destinée à polariser la grille (voir plus loin) dite résistance de fuite de grille ou grid-leak resistor.
    

Le courant ig est considéré comme nul pour le calcul du gain du fait qu’il est infiniment plus faible que les autres courants en jeu. En réalité il n’est pas nul sinon nous aurions vg = 0 ! La résistance de grille rg est très élevée au regard des autres valeurs de résistance , c’est pourquoi, au regard du calcul du gain elle est considérée comme infinie.

La résistance R0 étant traversée par le courant ig quasi nul n’intervien tpas sous cette forme dans l’impédance d’entrée. C’est donc la résistance RG qui représente l’impédance d’entrée du montage en principe. Celle-ci est souvent de l’ordre d’un mégohms.

Donc jusqu’ ici  \(Z_e = \frac{V_e}{IG}= RG\)

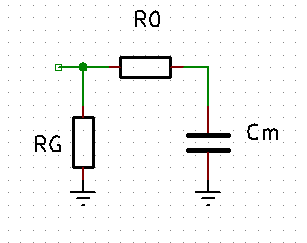
Dans la réalité l’impédance d’entrée est influencée également par les capacités inter-électrodes de la triode. Il existe en effet, comme le montre le schéma ci-dessous deux capacités , une Cga entre la grille et l’anode et l’autre Cgk entre grille et cathode qui sont traversées par le signal :

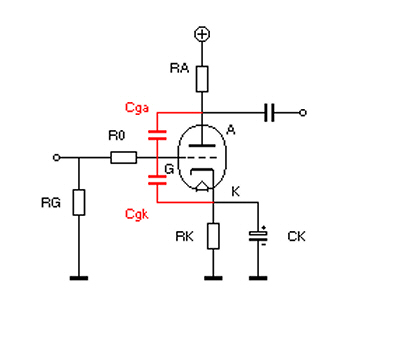
Naturellement pour raisonner il est nécessaire de retourner au schéma équivalent pour l’alternatif :

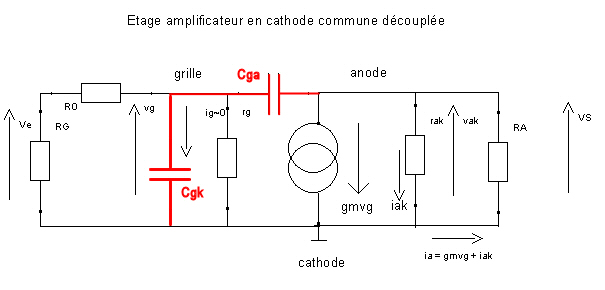
Les deux capacités mises en évidence sur le schéma ci-dessus sont caractéristiques du type de triode utilisée et figurent dans la datasheet.  Exemple pour l’ECC83 / 12 AX 7: Cga = 1,7 pF et Cgk = 1,6 pF.

Pour mesurer l’influence de ces capacités sur le signal, il suffit d’utiliser le résultat du théorème de Miller
démontré ici. L’application directe nous apprend que Cga se retrouve en parallèle de Cgk mais multipliée par 1 – A , A étant le gain négatif de l’étage (revoir ceci au besoin) soit par A + 1. Avec un gain de l’ordre de 50 pour ce montage nous avons la capacité d’entrée Ce = Cgk + 50 x Cga =par exemple pour l’ECC83 :1,6 + 50 x 1,7 pF = 86,6 pF.

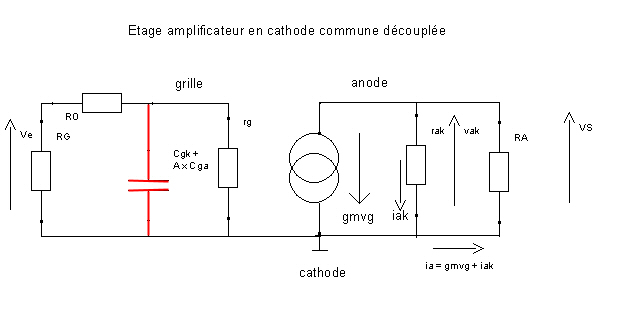
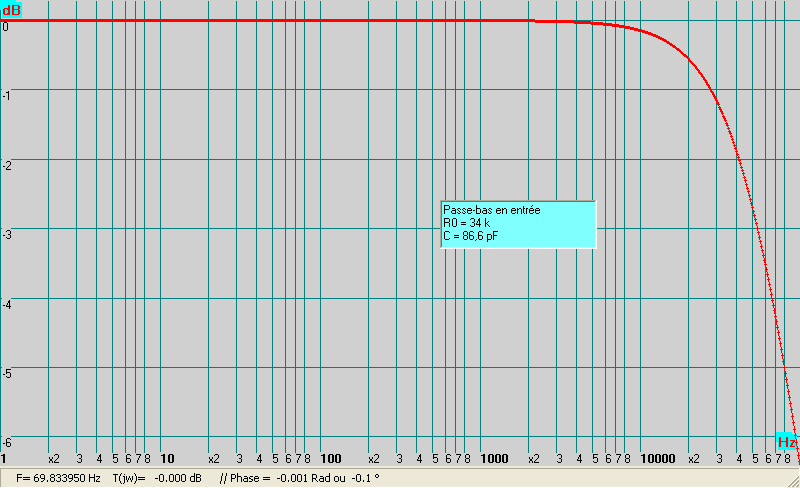
Il apparait tout de suite un filtre passe-bas composé de cette nouvelle capacité et de la résistance R0 que nous négligions tout à l’heure ! L’impédance d’entrée Ze du montage amplificateur en triode réside en fait dans ce passe-bas en parallèle sur RG.  Ze dépend donc de la fréquence .La fréquence de coupure à -3dB est donnée par

\(f_c = \frac {1}{2 \pi R C}\)

Exemple de conséquence : Prenons l’ exemple de l’étage d’entrée d’un préamplificateur où nous avons souvent pour R0 deux résistances en parallèle de 68k soit 34k. Le micro de la guitare est un générateur ( deThévenin !) dont l’impédance de sortie est de l’ordre de 3 ko, en série donc avec la résistance R0 de 34 ko soit 37 ko pour former le passe-bas avec 86.6 pF. La fréquence de coupure, si le volume de la guitare est à fond est alors de 49700 Hz soit largement dans les ultrasons.

 

Si l’on baisse le volume de la guitare équipée par exemple d’un humbucker dont le potentiomètre est souvent de 500 ko logarithmique on augmente l’impédance de sortie de l’ensemble. Un potentiomètre logarithmique gradué de 0 à 10 présente son impédance maximale de sortie au curseur autour de la graduation 7 et celle-ci est le quart de sa valeur soit ici 500k/4 = 125 ko.

On note alors une perte audible relative dans les aigus car la résistance R0 de 34 ko est alors en série avec 125 ko soit 159 ko au total et la fréquence de coupure devient fc = 1 / 2 x PI x 159000 x0,0000000000866 = 11600 Hz.

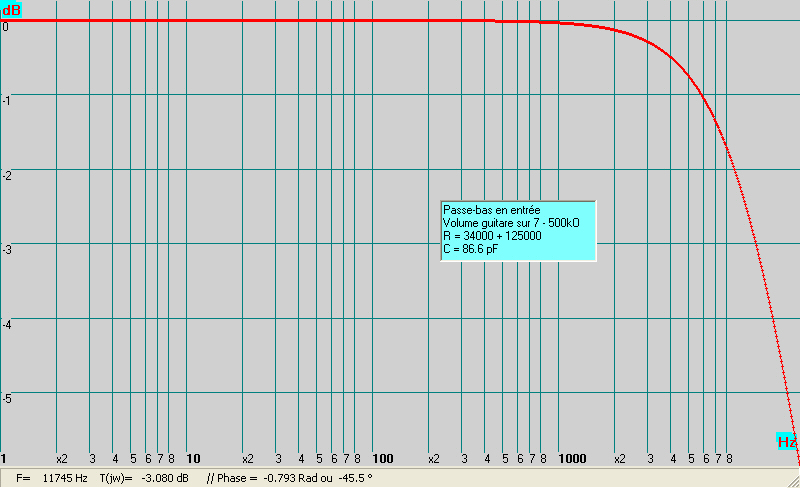
(contrairement à une idée reçue les aigus ne s’atténuent plus au-delà de la graduation 7 davantage que les fréquences basses, l’atténuation des aigus rejoignant l’atténuation générale au fur et à mesure que l’on tourne le potentiomètre vers 0).

Autre remarque : ceci explique que certains ajoutent sur le potentiomètre du volume de leur guitare une capacité reliant le micro au curseur pour shunter cette impédance sur l’entrée de l’ampli.

CONCLUSION :

Il est d’usage de qualifier les montages en utilisant une fréquence de référence de 1 kHz. On donne ainsi l’impédance d’entrée du montage pour cette fréquence. Cette impédance est une impédance complexe constituée du réseau suivant :

• une résistance R0 ( ou Rgs pour Rgrid-stopper) en série avec une capacité dite de Miller d’impédance \(\frac {1}{jC\omega} = \frac {1}{j (Cgk + (A+1)Cga)2\pi F} \)
• la résistance de polarisation de la grille RG (ou Rgl pour Rgrid-leak) qui vient en parallèle de l’impédance complexe ci-dessus.

Ze est donc un nombre complexe dont le calcul précis n’est pas immédiat* : la gain A utilisé pour le calcul de Cm est en principe dépendant de la fréquence mais on peut prendre la valeur correspondant à la bande passante A = -µRA /RA + rak car l’erreur ainsi faite pour les basses fréquences est non critique (ZCm est alors de l’ordre de 15 à 20 Mohms !).

 

\(Z_e = \frac {(R_0 + \frac{1}{j C_m \omega}) R_G} {R_0 + \frac{1}{j C_m \omega} + R_G}\)

 

 

\(Z_e = \frac {R_0 R_G j C_m \omega + R_G} {(R_0 + R_G) j C_m \omega + 1}\)

 

\(|Z_e| = \frac {\sqrt{R_0^2  R_G^2 C_m^2 \omega^2+R_G^2}} {\sqrt{(R_0 + R_G)^2 C_m^2 \omega^2+ 1}}\)

On calcule pour f = 1 kHz soit w = 2 pi x 1000 dans l’exemple de l’étage d’entrée ci-dessus avec :

• R0 = 34 ko
  
• Cm = 86,6 pF
  
• RG = 1 Mo

nous obtenons Ze = 871678 ohms . Pour une fréquence de 10 kHz cette impédance descend à 178 kohms.

En règle générale on peut estimer à 1 kHz une impédance d’entrée de l’ordre de 850 kohms

(* voir ici l’erreur à ne pas commettre)

Impédance de sortie

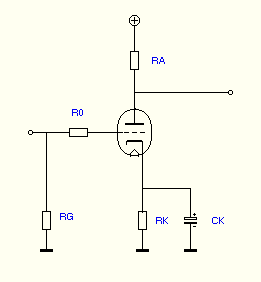Fig 1

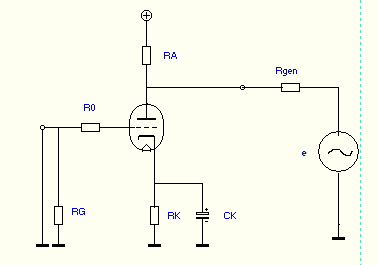
Fig 2

L’impédance de sortie se mesure comme vu ici en utilisant un générateur de tension sur la sortie dont la propre impédance de sortie est idéalement nulle ( Rgen=0). cf figure 2

On met alors l’entrée en court circuit. Le schéma équivalent pour l’alternatif Fig 3 montre les courants et tensions en jeu.

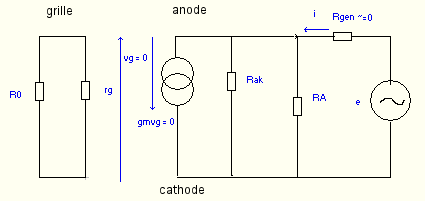
Fig 3

Avec la cathode complètement découplée RK//ZCk = 0 et rak est à la masse tout comme la cathode.

Le courant traversant rg ,résistance interne de grille, est nul et ainsi vg = 0 ainsi que gmvg le courant résultant.

L’impédance de sortie est donc le quotient e/i et on voit clairement sur le schéma résultant Fig 4 que l’impédance vue par le générateur est  RA // rak.

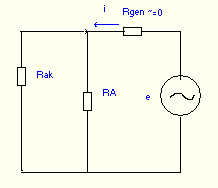
Fig 4

 

\(Z_S = \frac {RA rak} {RA+rak}\)

Exemple : un étage en triode 12AX7 (ECC83) à cathode commune complètement découplée avec une charge de 100 k à l’anodeet une résistance anode-cathode de 62500 ohms présente une impédance de sortie de 100 000 x 62500 / 162500 = environ 38500 ohms.

 

Bande passante

La bande passante d’un étage amplificateur à triode en cathode commune parfaitement découplée est entièrement liée à la capacité de Miller en entrée de l’étage. En sortie la fréquence de coupure haute est toujours très largement au-dessus de la bande audible de 20 Hz à 20 kHz.

Cette fréquence de coupure haute est donc uniquement tributaire de l’impédance de sortie de l’étage précédent ou du système du micro guitare , en série avec la résistance de grid-stopper de l’étage.

On se reportera donc à l’article sur l’impédance d’entrée de ce type de montage.

 

---

 

 

Amplificateur à triode en cathode commune partiellement découplée

Ce cas traite également le cas de la résistance de cathode Rk non découplée. Il suffit dans le raisonnement de remplacer l’impédance complexe Zk = Rk // Ck par une impédance résistive pure Rk.

• gain
• impédance d’entrée
• impédance de sortie
• bande passante

Calcul du gain

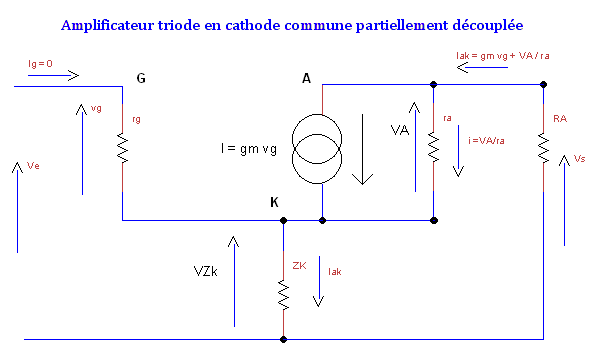
Avec :

• • ra = résistance interne de la triode  ( cf Datasheet)
  • VA = tension anode – cathode
  • gm = transconductance ( cf Datasheet)
  • Zk = impédance complexe sur la cathode ( Rk // Ck :  condensateur impédant )
  • RA l’impédance de charge sur l’anode
  • rg = résistance de grille considérée comme infinie

On part de la formule fondamentale donnant le courant de l’anode à la cathode. \(I_(ak) = gm vg + \frac {VA}{ra}\)  Le problème est de calculer le gain : \(A_v =  \frac {V_s}{V_e}\) Il faut pour cela exprimer Vs et Ve en fonction de vg mais d’abord éliminer l’inconnue VA : On constate :    \(V_s = – I_ak RA = -(gm vg + \frac {VA}{ra}) RA\)   d’où : \(\frac {V_s}{RA} + gm vg = -\frac {VA}{ra}\)   et donc (1) \(VA = -ra (\frac {V_s}{RA} + gm vg )\)   (2)   \(V_s = V_zk + VA\) Le courant de grille étant nul ( voir note ) , l’impédance Zk est traversée par le même courant Iak qui traverse RA donc et directement en fonction de Vs :        à partir de (1) et (2) on peut écrire en remplaçant VA par sa valeur en fonction de Vs :   sachant que gm ra = µ : On tire :         (3)       On applique le même principe pour calculer Ve sachant que l’on connaît maintenant Iak à partir de Vs  c-à-dire   Iak = – Vs / RA et que  Ve = vg + Vzk :     Ve = vg + Iak Zk (4)    Le gain Av = Vs / Ve étant le quotient de  (3) sur (4) :     Cette formule va servir à calculer précisément la fréquence de coupure basse induite par la capacité de découplage Ck. On peut maintenant représenter le montage complet ramené au générateur de Thévenin équivalent avec la tension = – µVe et l’impédance de sortie = ra + (µ +1)Zk. Le montage est appliqué à la charge RA     Note : en réalité le courant ig n’est pas nul sinon vg serait nul également. De fait ig est très faible et négligeable devant les courants gmvg et VA/ra.  C’est la résistance de grille rg qui est très élevée.

 

Calcul de l’impédance d’entrée

Calcul de l’impédance de sortie

Calcul de la bande passante